Spaces, Propagators, and Constraint Stores

The computational architecture for constraint propagation is called a space and consists of a number of propagators connected to a constraint store:

Figure 1: A computational architecture for Constraint Propagation

The constraint store stores a conjunction of basic constraints up to logical equivalence. An example for such a conjunction is

$X \in \ensuremath{\{0,\dots,5\}} \hspace{2mm}\wedge{} \hspace{2mm}Y=8 \hspace{2mm} \wedge{}\hspace{2mm} Z \in \ensuremath{\{13,\dots,23\}}.$

The propagators impose nonbasic constraints, for instance,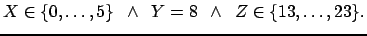

X < Y , X = Y or X² + Y² = Z².

A propagator for a constraint C is a computational agent that tries to narrow the domains of the variables occurring in C.

Two propagators that share a variable X can communicate with each other through the constraint store. To see an example for communicating propagators, suppose we have two propagators imposing the constraints

X + Y = 9   2 ^. X + 4 ^. Y = 24

over a constraint store containing the following information about X and Y:

$X \in \ensuremath{\{0,\dots,9\}} \hspace{4mm} Y \in \ensuremath{\{0,\dots,9\}}$

As is, the first propagator cannot do anything. The second propagator, however, can narrow the domains of both X and Y:

$X \in \ensuremath{\{0,\dots,8\}} \hspace{4mm} Y \in \ensuremath{\{2,\dots,6\}}$

Now the first propagator can narrow the domain of X: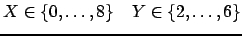

$X \in \ensuremath{\{3,\dots,7\}} \hspace{4mm} Y \in \ensuremath{\{2,\dots,6\}}$

Now the second propagator can narrow the domains of both X and Y: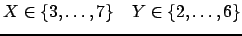

$X \in \ensuremath{\{4,\dots,6\}} \hspace{4mm} Y \in \ensuremath{\{3,4\}}$

This once more activates the first propagator, which narrows the domain of X: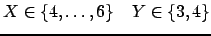

$X \in \ensuremath{\{5,\dots,6\}} \hspace{4mm} Y \in \ensuremath{\{3,4\}}$

Now the second propagator gets active once more and determines the values of X and Y: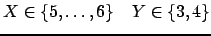

X = 6   Y = 3

Given a constraint store storing a constraint S and a propagator imposing a constraint P, the propagator can tell to the constraint store a basic constraint B if the conjunction S $\wedge$ P entails B and B adds new and consistent information to the store. To tell a constraint B to a constraint store storing the constraint S means to update the store so that it holds the conjunction S $\wedge$ B.

The operational semantics of a propagator determines whether the propagator can tell the store a basic constraint or not. The operational semantics of a propagator must of course respect the declarative semantics of the propagator, which is given by the constraint the propagator imposes.

We require that the constraint store be always consistent; that is, there must always be at least one variable assignment that satisfies all constraints in the constraint store.

We say that the constraint store determines a variable x if the constraint store knows the value of x, that is, if there exists an integer n such that the constraint store entails x = n.

We say that a propagator is inconsistent if there is no variable assignment that satisfies both the constraint store and the constraint imposed by the propagator (e.g., X + Y = 6 over $X \in \ensuremath{\{3,\dots,9\}}$ and $Y \in \ensuremath{\{4,\dots,9\}}$). We say that a propagator is failed if its operational semantics realizes that it is inconsistent.

We say that a propagator is entailed if every variable assignment that satisfies the constraint store also satisfies the constraint imposed by the propagator (e.g., X < Y over $X \in \ensuremath{\{3,\dots,5\}}$ and $Y \in \ensuremath{\{6,\dots,9\}}$). As soon as the operational semantics of a propagator realizes that the propagator is entailed, the propagator ceases to exist.

We require that the operational semantics of a propagator detects inconsistency and entailment at the latest when the store determines all variables of the propagator.

We say that a space is failed if one of its propagators is failed.

We say that a space is solved if all variables occuring in it are determined.

When a space is created, its propagators start to tell basic constraints to the constraint store. This propagation activity continues until a fixpoint is reached. An important property of constraint propagation as we consider it here is the fact that the order in which the propagators tell information to the store does not matter. When we start a space repeatedly from the same state, it will either always fail or always arrive at the same constraint store (up to logical equivalence).

A variable assignment is called a solution of a space if it satisfies the constraints in the constraint store and all constraints imposed by the propagators. The solutions of a space stay invariant under constraint propagation and deletion of entailed propagators.