1 Introduction
Constraints play an important role in the formulation of modern linguistic theories. For example HPSG and LFG are overtly constraint-based: they are primarily concerned with the formulation of general structural principles that determine the class of syntactically well-formed entities, typically represented as hierarchical, possibly typed, feature structures.
Yet, practical implementations are usually not driven but merely aided by constraints. For example implementations of HPSG typically only use constraints in the form of type hierarchies and unification, but the backbone remains generative (e.g. CFG).
The purpose of this course is to illustrate how constraints can be put into the driver's seat. We will shun merely constraint-aided approaches: these have been adequately presented by others in a Logic Programming setting. Instead we will focus on purely constraint-based approaches, where computation is reduced to constraint satisfaction.
While Prolog has proven to be a versatile implementation platform for computational linguistics, it encourages a view of computation as a non-deterministic generative process: typically a Prolog program specifies how to generate models. Regrettably, this often leads to difficult problems of combinatorial explosion.
In this course we wish to promote an alternative approach: replace model generation by model elimination. We will look at problems where the class of models is known before-hand and where constraints can be used to precisely characterize those which are admissible solutions: i.e. constraints serve to eliminate non-admissible candidates.
This course is by no means anti-Prolog: it is pro-constraints. Indeed, many of the techniques presented here are applicable to modern implementations of Prolog that support constraint libraries.
Some techniques, however, go beyond the capabilities of any Prolog system. This is primarily because Prolog does not support encapsulation or concurrency. In particular in does not support encapsulated speculative computations. Such notions where explored in AKL [Jan94], in the form e.g. of deep guards, but only reached their full potential in Oz, in the form of computation spaces [Sch97b] [Sch00]. We will use Oz as our programming vehicle [Smo95] [MMVR95].
The computational paradigm explored in this course, namely concurrent constraint programming, is the result of a historical progression that granted constraints an increasingly important role in computations:
- Generate and Test:
generate a candidate model and then verify that it solves the problem. Constraints are used only as post-hoc filters. Combinatorial explosion is fearsomely uncontrolled.
- Test and Generate:
generation and filtering are interleaved. Constraints typically remain passive but are successful in pruning entire branches of the search. This technique is often based on coroutined constraints using
freeze(akageler) introduced by Prolog II.- Propagate and Distribute:
constraints are active and perform as much deterministic inference as possible. The generative aspect is reduced to the minimum: the distribution strategy is invoked to make a choice only when propagation is not sufficient to resolve all ambiguities.
This progression results in increasingly smaller search trees. We can give an example that illustrates the improvements. Suppose that we are searching for solutions of the equation 2*A=B where A and B denote integers between 0 and 9 inclusive. Let us first consider a generate and test solver written in Oz: it picks values for variables A and B and only then checks whether these values satisfy the equation:
- <Equation Solver: generate and test>=
proc {EquationSolver1 Solution}
[A B] = Solution
in
Solution:::0#9
{FD.distribute naive Solution}
2*A=B
end
What you see above is a named code chunk. This form of code presentation, in small named chunks that are individually explained in the text, was pioneered by Donald Knuth under the name of Literate Programming. We will use it constantly throughout this course.
The generate and test approach produces the search tree of size 199 shown below. Blue circles represent choice points, red squares failed nodes, and green diamonds solutions.
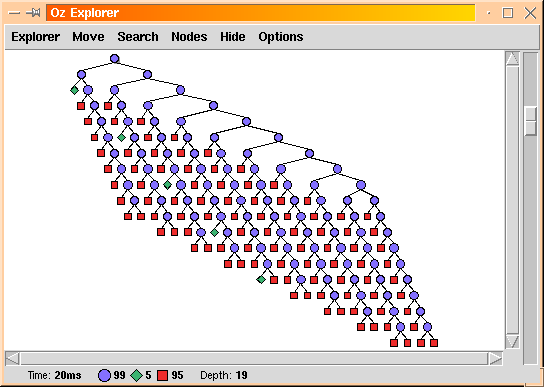
Now let's turn to the test and generate approach: the equation is posted in its own thread (i.e. the test is issued first) which suspends until a value has been chosen for A, at which the corresponding value for B can be computed.
- <Equation Solver: test and generate>=
proc {EquationSolver2 Solution}
[A B] = Solution
in
Solution:::0#9
thread 2*A=B end
{FD.distribute naive Solution}
end
The test and generate approach produces the search tree of size 19 shown below:
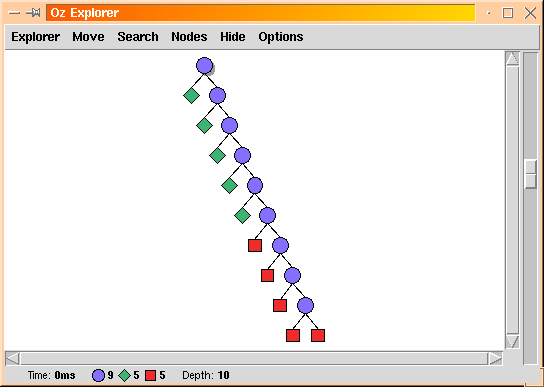
Finally, here is the real constraint programming way of solving the problem, using the propagate and distribute method. The equation is represented by a constraint:
- <Equation Solver: propagate and distribute>=
proc {EquationSolver3 Solution}
[A B] = Solution
in
Solution:::0#9
2*A=:B
{FD.distribute naive Solution}
end
The propagate and distribute approach produces the search tree of size 9 below. Note that this search tree contains no failed node.
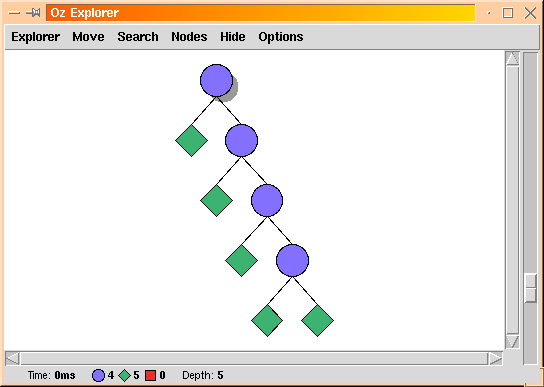
When writing this course, my first priority was to demonstrate how constraints can be used effectively in practice, for linguistic applications. As a result, for each topic, in addition to the formal presentation, I also provide the corresponding code. In each case, you get a complete interactive application that you can run, and whose code you can study. For reasons of space, the printed version of the course does not contain absolutely all the code, but almost. The online version contains absolutely everything and is available at:
http://www.ps.uni-sb.de/~duchier/esslli-2000/index.htmlThe online version also allows you to start the applications by clicking on appropriate links. Since Oz code forms a large part of the diet in this course, the reader is urgently advised to become marginally familiar with Oz. We highly recommend that you read at least The Oz Tutorial [HF99]. The Mozart system (implementing Oz) comes with a lot of online documentation, which is also available in Postscript or PDF for printing.