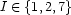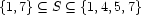6.2 Constraint Variables

Of particular relevance to this course are finite domain (FD) variables and finite set (FS) variables.

6.2.1 FD Variables

A FD variable 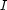denotes an integer out of a finite domain of possible values. In the store, it is represented by a basic constraint of the form e.g.:

$I\in\{1,2,7\}$

This is essentially a form of disjunction. Its declarative semantics are simply:

$I=1\quad\vee\quad I=2\quad\vee\quad I=7$

FD variables are a very economical and effective way to address certain forms of ambiguity arising in computational linguistics. Any finite collection of values/objects can be encoded as a finite domain: therefore an underspecified element of this collection can be represented by a FD variable. In Chapter 3, we illustrate this idea for agreement in German.

6.2.2 FS variables

A FS variable 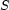denotes a finite set of integers. In the store it is represented by a basic constraint providing information about lower and upper bounds:

$\{1,7\}\subseteq S\subseteq\{1,4,5,7\}$

Again, this a form of disjunction: 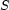may take as value any set that contains at least 1 and 7, and at most 1, 4, 5 and 7. Sets are incredibly useful in computational linguistic applications: (1) they permit elegant and succinct axiomatizations, (2) these axiomatizations are also efficient constraint programs.