3.3.1 Establishing a bijection between tuples and integers
Consider  domains
domains 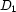 through
through 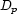 . Each domain
. Each domain 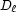 has cardinality
has cardinality 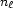 :
:
The cardinality of the cartesian product 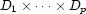 is
is 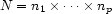 . We are going to establish a bijection between
. We are going to establish a bijection between 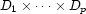 and
and ![[1.\,.N]](latex68.gif) .
.
The idea is to partition the interval ![[1.\,.N]](latex68.gif) into
into 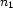 equal subintervals: one for each value in
equal subintervals: one for each value in 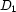 . Then to partition each subinterval into
. Then to partition each subinterval into 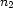 subsubintervals: one for each value in
subsubintervals: one for each value in 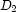 . Etc recursively.
. Etc recursively.
It is easy to capture this idea in a formula. Consider a tuple 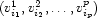 . According to the recursive algorithm outlined above, it is assigned to the following integer:
. According to the recursive algorithm outlined above, it is assigned to the following integer:
Thus, given an index 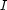 in the range
in the range ![[1.\,.N]](latex68.gif) , we can recover the corresponding tuple by calling
, we can recover the corresponding tuple by calling {DecodeInt I-1 Divs Doms}, where Divs is the list:
and Doms is the list of domains, each one consisting of a list of values. The function DecodeInt is implemented as follows:
- <DomainProduct DecodeInt function>=
fun {DecodeInt I Divs Doms}
case Divs#Doms
of nil#nil then nil
[] (Div|Divs)#(Dom|Doms) then
Q = I div Div
R = I mod Div
in
{Nth Dom Q+1}|{DecodeInt R Divs Doms}
end
end
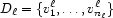
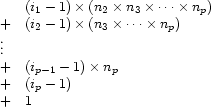
![\begin{array}{r@{}r@{}l}
[&n_2\times n_3\times\cdots\times n_p&\\
&n_3\times\cdots\times n_p&\\
\multicolumn{3}{c}{\vdots}\\
&n_p&\\
&1&]
\end{array}](latex74.gif)