3.6.1 Selection Constraint

In this section, we very briefly introduce the idea of the selection constraint for finite domains. It has the form:

I={Select.fd [I1 I2 ... In] K}

where I, I1, ..., In, K are all FD variables (possibly determined, i.e. integers). Its declarative semantics is that 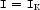$\text{\texttt{I}}=\text{\texttt{I}}_{\text{\texttt{K}}}$ . Constraint propagation can affect both I and K: if Ip cannot be equal to I (i.e. their domains are disjoint), then p is removed from the domain of K. Furthermore, the domain of I must be a subset of the union of the domains of Ip for p in the domain of K. To learn more about the selection constraint, see Section 6.9 and also the treatment of dependency parsing in Chapter 5.