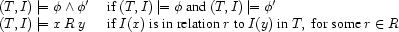4.2.1 Models of Dominance Constraints

A model of a dominance constraint 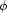$\phi$ is a pair 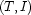(T,I) of a tree 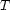and an interpretation of 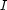mapping variables of 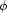$\phi$ to nodes in 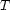, and such that 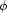$\phi$ is satisfied. We write 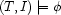$(T,I)\models\phi$ to say that 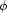$\phi$ is satisfied by 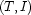(T,I) and define it in the usual Tarskian way as follows:

$\begin{array}{ll} (T,I)\models \phi\wedge\phi' &\text{ if } (T,I)\models\phi\text{ and }(T,I)\models\phi'\\ (T,I)\models x\mathbin{R} y&\text{ if } I(x) \text{ is in relation } r \text{ to } I(y) \text{ in } T, \text{ for some } r\in R \end{array}$

Solving dominance constraints is NP-hard. This was shown e.g. in [KNT98] by encoding boolean satisfiability as a dominance problem. However, the constraint-based technique first outlined in [DG99] has proven quite successful and solves practical problems of arising e.g. in semantic underspecification very efficiently. The technique is formally studied and proven sound and complete in [DN00]. An extension of this technique to handle general descriptions with arbitrary Boolean connectives was presented in [Duc00].