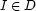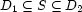2.2 Constraint-based Representation of Assignments
The types of problems that constraint programming is really good at are all about integers. This is where constraints are able to provide strong and efficient propagation.
Constraints involving Finite Domains have become a fairly standard tool of the trade. More recently, constraints on Finite Sets (of integers) have appeared [Ger95] [MM97] [Mül98] and proven to be extremely expressive, especially for applications in computational linguistics [Duc99a] [Duc99b]. In this course, we will see many applications of set constraints.
Thus, we will consider CSPs involving integer variables (written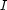 
) and set variables (written 
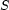). The fundamental idea of the constraint programming approach is to explicitly represent the partial information about the sought assignment. For example, we may not precisely know the value to be assigned to 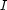, but we may know that it must be either 2, 3, or 7. Thus we would write 
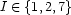. The general form of the partial information about the assignment to an integer variable is thus:
where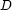 
is a domain, i.e. a given finite set of integers.
Similarly, we may not know precisely which set value to assign to a set variable 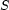, but we may have some information about its lower and upper bounds (i.e. the integers at least, resp. at most, in ). Thus we write:
