Disjunctive Propagator

In Logic Programming, the only method available for dealing with complex disjunctions is non-determinism. Thus, in Prolog, you would write:

C1 ; C2

and this would have the effect to first try C1, and then on backtracking to try C2. In other words, in Prolog you must commit very early to exploring either one alternative or the other.

Early commitment is a poor strategy in general. In many cases, it would be preferable to delay this choice until e.g. sufficient information is known to reject one alternative altogether. This is the intuition behind the disjunctive propagator:

C1 or C2

It is a propagator, not a choice point! C1 and C2 are arbitrary constraints: when one of them becomes inconsistent with what is currently known (i.e. with the store of basic constraints), then the propagator reduces to the other one. Thus, a disjunctive propagator has the declarative semantics of sound logical disjunction (unlike Prolog's ; operator which depends on negation as failure) and the operational semantics given by the rules below:

$\begin{array}{@{}rll@{}} \mathcal{B}\wedge C_1&\rightarrow^*&\textsf{false}\\\hline \mathcal{B}\wedge(C_1\ \textbf{or}\ C_2)&\rightarrow&\mathcal{B}\wedge C_2\\[2mm] \mathcal{B}\wedge C_2&\rightarrow^*&\textsf{false}\\\hline \mathcal{B}\wedge(C_1\ \textbf{or}\ C_2)&\rightarrow&\mathcal{B}\wedge C_1 \end{array}$

How is this possible? We have already explained that all computations operate over a constraint store. We can go one better and allow nested constraint stores. This idea is indeed supported by Oz under the name of Computation Spaces (see Section 6.4). The disjunctive propagator C1 or C2 creates 2 nested computation spaces - one in which to execute C1 and one in which to (concurrently) execute C2 - and it monitors both spaces. If an inconsistency is derived in the space where, say, C2 executes, then the space where C1 executes is simply merged with the current space, thus committing to alternative C1.

A disjunctive propagator C1 or C2 allows to delay the choice between the two alternative in the hope that constraint propagation alone will be able to decide it. However, this may fail to happen, in which case, to ensure completeness, we may have to non-deterministically force the choice anyway. How can we achieve this?

The usual technique is to introduce a Control Variable, i.e. a finite domain variable whose purpose is simply to allow to choose the alternative. For example, you might write:

X=1 C1 or X=2 C2

Thus, if constraint propagation is unable to decide the disjunction either way, you can non-deterministically either try X=1 or try X=2. Variable X allows you to control the disjunction.

In the case of the well-formedness clauses, we already have the variables 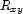$R_{xy}$ which can serve this purpose.