init method

The init method initializes the attributes and then processes each literal of the description, creating the corresponding problem-specific constraints. A literal is processed simply by invoking it as method on the solver object. The first time that variable is encountered, it is assigned a new integer to encode it and its corresponding 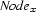is created. The nested loops create all well-formedness clauses for the variables encountered in the description. Finally, the first-fail distribution strategy is invoked to search for consistent assignments to the variables .

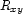<Dominance: Solver class, init method>=

meth init(Desc Info)
   var2int  <- {NewDictionary}
   int2node <- {NewDictionary}
   vars     <- {FS.var.decl}
   labs     <- {FS.var.decl}
   choices  <- {NewDictionary}
   for D in Desc do {self D} end 
   {CloseSet @vars}
   {CloseSet @labs}
   {self info(Info)}
   for I in 1..@counter do 
      for J in 1..(I-1) do 
         {Clauses @int2node.I @int2node.J @choices.(I*1000+J)}
      end 
   end 
   {FD.distribute ff {Dictionary.items @choices}}
end

Note that @vars and @labs are initially completely underspecified. Whenever a new variable is encountered, it is stated to be an element of @vars. Whenever a labeling constraint is encountered, the labeled variable is stated to be an element of @labs. When all literals have been processed, then all variables are known, and all explicitly labeled variables as well: CloseSet is invoked on both @vars and @labs to state that whatever is known to be in these sets sofar is really all there is (i.e. the lower bound is also the upper bound).

<Dominance: utilities>= >>

proc {CloseSet S}
   {FS.var.upperBound {FS.reflect.lowerBound S} S}
end