Next: Branching and Search Trees Up: Propagate and Branch Previous: Interval and Domain Propagation Contents
A straightforward example for the second case consists of three propagators for
Xand a constraint storeY X
Z Y
Z
This space has no solution. Nevertheless, none of the propagators is inconsistent or can tell something to the constraint store.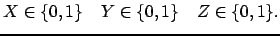
To see an example for the case where a unique solution is not found by constraint propagation, suppose we have interval propagators for the constraints
3 . X + 3 . Y = 5 . Z X - Y = Z X + Y = Z + 2and a constraint store
This space has the unique solution X = 4, Y = 1, Z = 3. Nevertheless, none of the propagators can narrow a variable domain.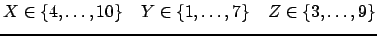
If we narrow the domains to
the space becomes unsatisfiable. Still, none of the above propagators is inconsistent or can narrow a variable domain.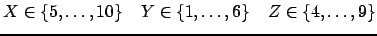
Andreas Rossberg 2006-08-28