An Example

To see the outlined propagate and branch method at a concrete example, consider the problem specified by the following constraints:

X $\neq$ 7   Z $\neq$ 2   X - Z = 3 ^. Y
$X \in \ensuremath{\{1,\dots,8\}} \hspace{4mm} Y \in \ensuremath{\{1,\dots,10\}} \hspace{4mm} Z \in \ensuremath{\{1,\dots,10\}}$

To solve the problem, we start with a space whose store constrains the variables X, Y, and Z to the given domains. We also create three propagators imposing the constraints X $\neq$ 7, Z $\neq$ 2, and X - Z = 3 ^. Y . We assume that the propagator for X - Z = 3 ^. Y realizes interval propagation, and that the propagators for the disequations X $\neq$ 7 and Z $\neq$ 2 realize domain propagation.

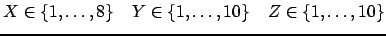
The propagators for the disequations immediately write all their information into the store and disappear. The store then knows the domains

$X \in [\ensuremath{\{1,\dots,6\}} ; 8] \hspace{4mm} Y \in \ensuremath{\{1,\dots,10\}} \hspace{4mm} Z \in [1 ; \ensuremath{\{3,\dots,10\}}]$

where $[1 ; \ensuremath{\{3,\dots,10\}}]$ denotes the finite domain {1} $\cup$ {3,..., 10}. The interval propagator for X - Z = 3 ^. Y can now further narrow the domains to

$X\in[\ensuremath{\{4,\dots,6\}} ; 8] \hspace{4mm} Y \in \ensuremath{\{1,2\}} \hspace{4mm} Z\in[1 ; \ensuremath{\{3,\dots,5\}}].$

Now propagation has reached a fixpoint. Thus, we continue with a first branching step. We choose to branch with the constraint X = 4. Figure 3 shows the resulting search tree.

Figure 3: A search tree containing 3 choice nodes, 1 failure node, and 3 solution nodes.

The space obtained by adding a propagator for X = 4 can be solved by propagation and yields the solution

X = 4   Y = 1   Z = 1

The space obtained by adding a propagator for X $\neq$ 4 reaches a fixpoint immediately after this propagator has written its information into the constraint store, which then looks as follows:

$X \in [\ensuremath{\{5,\dots,6\}} ; 8] \hspace{4mm} Y \in \ensuremath{\{1,2\}} \hspace{4mm} Z \in [1 \; \ensuremath{\{3,\dots,5\}}]$

This time we branch with respect to the constraint X = 5.

The space obtained by adding a propagator for X = 5 fails since X - Z = 3 ^. Y is inconsistent with the store obtained by adding X = 5.

The space obtained by adding a propagator for X $\neq$ 5 reaches a fixpoint immediately after this propagator has written its information into the constraint store, which then looks as follows:

$X \in [6 \; 8] \hspace{4mm} Y \in \ensuremath{\{1,2\}} \hspace{4mm} Z \in [1 \; \ensuremath{\{3,\dots,5\}}]$

Now we branch with respect to the constraint X = 6.

The space obtained by adding a propagator for X = 6 can be solved by propagation and yields the solution

X = 6   Y = 1   Z = 3

Finally, the space obtained by adding a propagator for X $\neq$ 6 can also be solved by propagation, yielding the third and final solution

X = 8   Y = 1   Z = 5

An alternative to the propagate and branch method is a naive enumerate and test method, which would enumerate all triples (X, Y, Z) admitted by the initial domain constraints and test the constraints X $\neq$ 7, Z $\neq$ 2 , and X - Z = 3 ^. Y for each triple. There are 8 * 10 * 10 = 800 candidates. This shows that constraint propagation can reduce the size of the search tree considerably.