Finite Domains and Constraints

A finite domain is a finite set of integers. A constraint is a formula of predicate logic. Here are typical examples of constraints occurring with finite domain problems:

$X=67 \hspace{5mm} X\in\ensuremath{\{0,\dots,9\}} \hspace{5mm} X=Y$
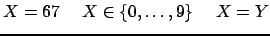
X² - Y² = Z²   X + Y + Z < U   X + Y $\neq$ 5 ^. Z
X₁,..., X₉ are pairwise distinct

A domain constraint (also called basic constraint) takes the form x $\in$ D, where D is a finite domain.

A finite domain problem is a finite set P of quantifier-free constraints such that P contains a domain constraint for every variable occurring in a constraint of P. A variable assignment is a function mapping variables to integers.

A solution of a finite domain problem P is a variable assignment that satisfies every constraint in P.

Notice that a finite domain problem has at most finitely many solutions, provided we consider only variables that occur in the problem (since the problem contains a finite domain constraint for every variable occurring in it).