6.5 Search

A major application domain for CP, and the only one that we look at in this course, is to solve constraint satisfaction problems (CSPs); i.e. to find assignment of values to variables such that a collection of constraints is satisfied.

The whole advantage of CP for solving CSPs rests on constraint propagation: let propagators improve the information in the store until no further improvement is possible (i.e. a fix point is reached). To improve the information in the constraint store means to reduce the number of possible values for each variable. This effectively reduces the search tree since after propagation there are fewer possible assignments to consider.

In fact, to solve a CSP, we proceed by alternating steps of propagation and distribution. If propagation is not sufficient to determine values for all variables, we may pick a variable X that is not yet determined, non-deterministically pick a value v from the set of those that remain after propagation, and assign it to the variable, i.e. tell the basic constraint X=v. X=v is new information, and again we let propagation derive as many improvements from it as possible. The non-deterministic cycle is repeated until all variables are determined.

In the preceding explanation, we postulated a non-deterministic process. This is standard in most LP and CP systems: a basic constraint X=v is non-deterministically chosen and added to the same global store. It may be removed and another one chosen on backtracking. Oz, however, offers an alternative. Since computation spaces are 1st class, we can make a copy and add X=v in the copy. This way, we don't have to backtrack on failure, we can just throw away the failed copy; we still have the original, and we can make another copy to try a different constraint, say X=a.

Thanks to this powerful idea, search in Oz is not built-in as in Prolog; instead it is programmed in Oz itself. The reader interested in how various search algorithms can be programmed in Oz is advised to read [Sch97b]. Search in Oz is guided by a distribution strategy. A distribution strategy is invoked when it is necessary to perform a distribution step. It is responsible for choosing a constraint 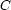(for example X=v above). The search engine then creates 2 copies of the current space: in the first copy it adds constraint 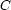and in the second copy it adds 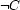. Thus, for above example, one branch of the search would explore the consequences of 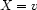and the other of .

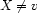The Mozart system offers rich libraries with predefined search engines and distribution strategies that cover most of the usual cases. The reader is strongly advised to read [SS99] which is an introduction to constraint programming in Oz. For some advanced topics, see also [SSW94] [SS94] [Sch97b] [Sch00].