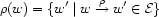Daughter Sets

We need to represent labeled edges between nodes. Traditionally, this is realized by means of feature structures: each node is a feature structure and an edge 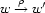$w\EDGE\rho w'$ is represented by the presence of a feature $\rho$ on 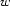, such that 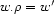$w.\rho=w'$ . This, however, is a lousy idea when the goal is to take advantage of active constraint propagation. The problem is that, in the traditional view, features are partial functions: i.e. 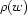$\rho$ is a partial function from nodes to nodes (from now on, we will write $\rho(w)$ instead of 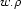$w.\rho$ ). It is rather inconvenient to try to express constraints on 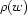$\rho(w)$ when it is not always defined!

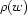However, a slight change of representation allows us to turn $\rho$ into a total function. Instead of $\rho(w)$ being either undefined or defined and denoting a node, we let it denote a set of nodes. Now instead of being undefined 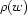$\rho(w)$ is simply empty. In the case where it was originally defined, it now denotes a singleton set.

Thus 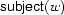$\Feature{subject}(w)$ denotes the set of subjects of 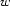: empty except when 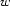is a finite verb, in which case it is a singleton. We say that 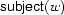$\Feature{subject}(w)$ is a daughter set of 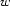, i.e. a set of daughters. This idea has the second advantage that, in addition to complements (like subject), it also naturally accommodates modifiers (like adjectives): 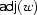$\Feature{adj}(w)$ is the set of adjectives of 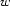. The difference is that a modifier daughter set may have any number of elements instead of at most 1 for a complement daughter set.

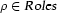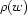Formally, for each role $\rho\in\setof{Roles}$ , we introduce a function $\rho$ such that $\rho(w)$ is the set of immediate daughters of 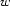whose dependency edge is labeled with $\rho$ :

$\rho(w)=\{w'\mid w\EDGE\rho w'\in\EE\}$

in the constraint model 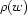$\rho(w)$ is a finite set variable.