Example: Sudoku Puzzle

History

Howard Garnes, a freelance puzzle constructor and retired architect, has designed the puzzle in 1979. It was first published in New York in the late 1970s by the specialist puzzle publisher Dell Magazines in its magazine Dell Pencil Puzzles and Word Games, under the title Number Place. The puzzle was introduced in Japan by Nikoli 1984 as "Suji wa dokushin ni kagiru", which can be translated as "the numbers must be single" or "the numbers must occur only once". (See here to get some more information)

Problem Description

Sudoku is a puzzle played on a partially filled 9 x 9 grid. The task is to complete the assignment using numbers from 1 to 9 such that the entries in each row, each column and each major 3 x 3 block are pairwise different. Below are given two tables (taken from the paper [8]); the first (3.3.2) is showing a Sudoku Problem and the second (3.3.2) a solution to this problem. By choosing a 'good' viewpoint, most instances of the Sudoku Puzzle can be solved without search.

2 6 8 1

3 7 8 6

4 5 7

5 1 7 9

3 9 5 1

4 3 2 5

1 3 2

5 2 4 9

3 8 4 6

7 2 6 4 9 3 8 1 5

3 1 5 7 2 8 9 4 6

4 8 9 6 5 1 2 3 7

8 5 2 1 4 7 6 9 3

6 7 3 9 8 5 1 2 4

9 4 1 3 6 2 7 5 8

1 9 4 8 3 6 5 7 2

5 6 7 2 1 4 3 8 9

2 3 8 5 7 9 4 6 1

Viewpoints for the Sudoku Problem

In the following two different approaches to model the Sudoku Problem are shown:

1. the variables x₁,..., x₈₁ represent all boxes in the grid, and the domain of each variable is the set of integers {1, ..., 9}, i.e. the values every box can have; an assignment x_i = c means that the i-th box has the value c.
2. the variables nb₁,..., nb₉ represent the numbers 1, ..., 9, and the domain of every number is the power set 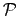$\mathcal {P}${1,..., 81}, i.e. the boxes a number occurs; an assignment nb_i = { c₁,..., c_n} means that number i occurs in box c₁,..., c_n and { c₁,..., c_n } is a subset of {1, ..., 81}.

In the first viewpoint you only need the propagator distinct(s,v) that is already implemented in the Alice library and that ensures that all elements of the vector v are distinct in space s, i.e. pairwise non-equal. To achieve the requirements of the Sudoku Problem you have to use the distinct propagator for each row, each column and each 3 x 3 box.

In the second viewpoint, rules are more awkward to express. You have to guarantee that the cardinality of every set representing a number is 9, that all those sets are disjoint, that every number has exactly one value in every row and every column and exactly one value in every 3 x 3 box.