Subsections
Alice provides finite sets of integers as
first-class values and every set value is a subset of
the universal set U = {- sup,...,sup}.
The value of sup is determined by the
actual implementation and in Alice it is 536870910.
A basic set constraint approximates a set value S
in three different ways:
- Constraining the lower bound by set s:s
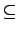 S.
The lower bound contains all elements that are at
least contained in the set value.
S.
The lower bound contains all elements that are at
least contained in the set value.
- Constraining the upper bound by set s :S
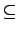 s .
The upper bound contains all elements that
are at most contained in the set value.
s .
The upper bound contains all elements that
are at most contained in the set value.
- Constraining the cardinality of a set by a finite
domain interval {n,...,m}: n
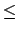 #S
#S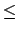 m .
The cardinality constraint determines the minimal
and maximal number of elements allowed to be contained in the set.
m .
The cardinality constraint determines the minimal
and maximal number of elements allowed to be contained in the set.
A set constraint denotes a set value if either the lower
is equal to the upper bound, the cardinality of the lower
bound is equal to the upper bound of the cardinality constraints,
or the cardinality of the upper bound is equal to the lower
bound of the cardinality constraint.
Non-basic set constraints, as intersubsection 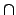 , union
, union 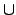 ,
disjointness ||,
and the like, are provided as propagators. For details on the provided
set propagators see the structure
FS.
,
disjointness ||,
and the like, are provided as propagators. For details on the provided
set propagators see the structure
FS.
To explain constraint propagation, assume the basic
set constraints:
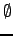
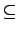 X,Y
X,Y 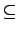 {1,...,5}
{1,...,5}
and additionally the following non-basic constraints:
X 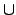 Y = {1,...,5} and X||Y.
Y = {1,...,5} and X||Y.
Adding the constraints 1 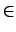 X and 2
X and 2 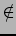 Y yields
the intermediate store {1}
Y yields
the intermediate store {1} 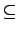 X
X 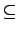 {1,...,5}
and
{1,...,5}
and
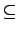 Y
Y 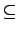 {1,3,4,5}. The
present non-basic constraints can add even more basic
constraints: the disjointness constraint removes 1 from
the upper bound of Y since 1 was added to the lower bound
of X. The union constraint adds 2 to the lower bound of
X since 2 was removed from the upper bound of Y.
After that, propagation has reached a fixed-point and leads to
{1,2}
{1,3,4,5}. The
present non-basic constraints can add even more basic
constraints: the disjointness constraint removes 1 from
the upper bound of Y since 1 was added to the lower bound
of X. The union constraint adds 2 to the lower bound of
X since 2 was removed from the upper bound of Y.
After that, propagation has reached a fixed-point and leads to
{1,2}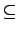 X
X 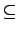 {1,...,5} and
{1,...,5} and
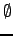
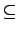 Y
Y 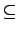 {3,4,5}.
Bringing the cardinality constraint 3
{3,4,5}.
Bringing the cardinality constraint 3 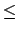 #Y
#Y 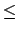 5
into play determines Y to {3,4,5} since the upper
bound has exactly 3 elements which is the minimal number
required by the cardinality constraint.
The disjointness constraint then removes 3, 4, 5 from X's
upper bound and that way determines x to {1,2}.
5
into play determines Y to {3,4,5} since the upper
bound has exactly 3 elements which is the minimal number
required by the cardinality constraint.
The disjointness constraint then removes 3, 4, 5 from X's
upper bound and that way determines x to {1,2}.
Set constraints on their own are of limited use, connecting
them with finite domain constraints provides much more
expressivity. The straightforward way is to connect a finite
set variable via the cardinality constraint to a finite
domain variable. Another technique is to provide reified
versions for various set constraints as containment and
the like. But there are further possiblies if the fact
that the elements of a set are integers is exploited.
Due to the fact that constraint propagation is incomplete,
expectedly in case of set constraints as well, solving a
problem involving set constraints requires branching.
A typical choice-point branching a set variable is
n 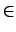 S
S 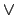 n
n 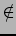 S.
The following figure illustrates that.
S.
The following figure illustrates that.
Figure 12:
Branching with set constraints
|
|
Andreas Rossberg
2006-08-28
![]() , union
, union ![]() ,
disjointness ||,
and the like, are provided as propagators. For details on the provided
set propagators see the structure
FS.
,
disjointness ||,
and the like, are provided as propagators. For details on the provided
set propagators see the structure
FS.
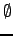
X,Y
{1,...,5}
Y = {1,...,5} and X||Y.