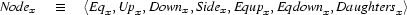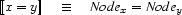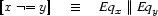Characteristic Set Constraints
In order to formulate the constraints that will only license tree-shaped solved forms, we must first consider each individual case 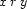 for
for 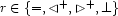 . For each case
. For each case 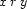 and its negation
and its negation 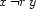 , we will formulate characteristic constraints involving the set variables that we introduced above.
, we will formulate characteristic constraints involving the set variables that we introduced above.
Let's consider the case 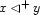 for which a solution looks as shown below:
for which a solution looks as shown below:
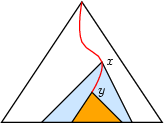
For convenience, we define, for each variable  , the additional set variables
, the additional set variables 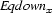 and
and 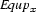 as follows:
as follows:
We write 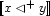 for the constraint characteristic of case
for the constraint characteristic of case 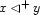 and define it as follows:
and define it as follows:
I.e. all variables equal or below  are below
are below  , all variables equal or above
, all variables equal or above  are above
are above  , and all variables disjoint from
, and all variables disjoint from  are also disjoint from
are also disjoint from  . This illustrates how set constraints permit to succinctly express certain patterns of inference. Namely
. This illustrates how set constraints permit to succinctly express certain patterns of inference. Namely 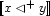 precisely expresses:
precisely expresses:
The negation is somewhat simpler and states that no variable equal to  is above
is above  , and no variable equal to
, and no variable equal to  is below
is below  . Remember that
. Remember that 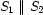 expresses that
expresses that 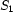 and
and 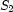 are disjoint.
are disjoint.
We can define the other cases similarly. Thus 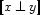 :
:
and its negation 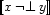 :
:
For the case 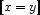 we first introduce notation. We write
we first introduce notation. We write 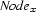 for the tuple defined as follows:
for the tuple defined as follows:
where 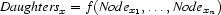 when the constraint
when the constraint 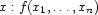 occurs in
occurs in 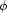 (more about this when presenting the problem-specific constraints). Now we can simply define
(more about this when presenting the problem-specific constraints). Now we can simply define 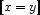 as:
as:
and its negation 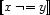 as:
as:
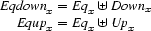
![\ENC{x\LT y}\quad\equiv\quad
\begin{array}[t]{@{}cl@{{}\subseteq{}}l}
&\EQDOWNV{y}&\DOWNV{x}\\
\wedge&\EQUPV{x}&\UPV{y}\\
\wedge&\SIDEV{x}&\SIDEV{y}
\end{array}](latex141.gif)
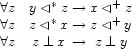
![\ENC{x\NLT y}\quad\equiv\quad
\begin{array}[t]{@{}cl}
&\EQV{x}\PAR\UPV{y}\\
\wedge&\EQV{y}\PAR\DOWNV{x}
\end{array}](latex144.gif)
![\ENC{x\DJ y}\quad\equiv\quad
\begin{array}[t]{@{}cl}
&\EQDOWNV{x}\subseteq\SIDEV{y}\\
\wedge&\EQDOWNV{y}\subseteq\SIDEV{x}
\end{array}](latex146.gif)
![\ENC{x\DJ y}\quad\equiv\quad
\begin{array}[t]{@{}cl}
&\EQV{x}\PAR\SIDEV{y}\\
\wedge&\EQV{y}\PAR\SIDEV{x}
\end{array}](latex148.gif)