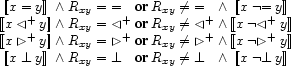Well-Formedness Clauses

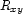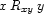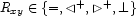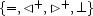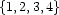For every pair of variables and , we introduce a finite domain variable $R_{xy}$ to denote the relationship $x\mathbin{R_{xy}}y$ that obtains between them. $R_{xy}\in\{\EQ,\LT,\GT,\DJ\}$ and we freely identify $\{\EQ,\LT,\GT,\DJ\}$ with $\{1,2,3,4\}$ . In a solved form, every 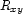$R_{xy}$ must be determined.

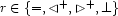In order to guarantee that a solved form is tree-shaped, for each pair of variables and , we consider the 4 mutually exclusive possibilities. For each possible relation $r\in\{\EQ,\LT,\GT,\DJ\}$ we state that either 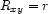$R_{xy}=r$ and the corresponding characteristic constraints 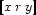$\ENC{x\mathbin{r}y}$ hold, or 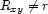$R_{xy}\neq r$ and the constraints 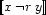$\ENC{x\mathbin{{\neg}r}y}$ characteristic of the negation hold.

Thus for each pair of variables and , we stipulate that the following 4 Well-Formedness Clauses hold:

$\begin{array}{@{}c@{{}\wedge{}}l@{\ \textbf{or}\ }l@{{}\wedge{}}c@{}} \ENC{x\EQ y}& R_{xy}=\EQ & R_{xy}\neq\EQ&\ENC{x\NEQ y}\\ \ENC{x\LT y}& R_{xy}=\LT & R_{xy}\neq\LT&\ENC{x\NLT y}\\ \ENC{x\GT y}& R_{xy}=\GT & R_{xy}\neq\GT&\ENC{x\NGT y}\\ \ENC{x\DJ y}& R_{xy}=\DJ & R_{xy}\neq\DJ&\ENC{x\NDJ y} \end{array}$

These clauses are all of the form 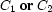$C_1\textbf{ or }C_2$ . This denotes a disjunctive propagator and is explained in the next section.