Getting Started

Reification of a constraint

The reification of a constraint C with respect to a variable x is the constraint

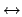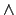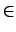( C $\leftrightarrow$ x = 1) $\wedge$ x $\in$ 0#1

where it is assumed that x does not occur free in C.

The operational semantics of a propagator for the reification of a constraint C with respect to x is given by the following rules:

1. If the constraint store entails x = 1, the propagator for the reification reduces to a propagator for C.
2. If the constraint store entails x = 0, the propagator for the reification reduces to a propagator for 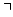$\urcorner$ C.
3. If a propagator for C would realize that the constraint store entails C, the propagator for the reification tells x = 1 and ceases to exist.
4. If a propagator for C would realize that the constraint store is inconsistent with C, the propagator for the reification tells x = 0 and ceases to exist.

To understand these rules, you need to be familiar with the definitions in Section 2.2.

0/1-variables

A 0/1-variable is a variable that is constrained to the finite domain 0#1. The control variables of reified constraints are 0/1-variables.

Posting reified constraints

Here are examples for statements creating propagators for reified constraints:

• Reified.intvar (s, dom, b)
  Returns an FD variable freshly created in s. Also, a propagator is created to ensure b is true if and only if the intvar returned is in dom.
• Reified.intvarVec (s, n, dom, b)
  Returns a vector of FD variables freshly created in s. Also, a propagator is created to ensure b is true if and only if all the intvars returned are in dom.
• Reified.dom (s, x, dom, b)
  Creates a propagator in s to ensure b is true if and only if x is in dom.
• Reified.rel (s, x, rel, y, b),Reified.relI (s, x, rel, n, b)
  Creates a propagator in s to ensure b is true if and only if x is in rel with y (or n).
• Reified.linear (s, v, rel, n, b, level)
  Creates a propagator in s to ensure b is true if and only if the regular linear constraint holds for the arguments.