Next: Problem Solving with Finite Up: Branch and Bound Previous: Example: Send Most Money Contents
We assume the fixed costs of building a warehouse to be 50. We furthermore assume 5 warehouses W1 through W5 and 10 stores Store 1 through Store 10. The capacities of the warehouses are:
| W1 | W2 | W3 | W4 | W5 | |
| capacity | 1 | 4 | 2 | 1 | 3 |
The costs to supply a store by a warehouse are:
| W1 | W2 | W3 | W4 | W5 | |
| Store 1 | 36 | 42 | 22 | 44 | 52 |
| Store 2 | 49 | 47 | 134 | 135 | 121 |
| Store 3 | 121 | 158 | 117 | 156 | 115 |
| Store 4 | 8 | 91 | 120 | 113 | 101 |
| Store 5 | 77 | 156 | 98 | 135 | 11 |
| Store 6 | 71 | 39 | 50 | 110 | 98 |
| Store 7 | 6 | 12 | 120 | 98 | 93 |
| Store 8 | 20 | 120 | 25 | 72 | 156 |
| Store 9 | 151 | 60 | 104 | 139 | 77 |
| Store 10 | 79 | 107 | 91 | 117 | 154 |
i
{1,..., 5}
j
{1,..., 10}: (Suppliesi, j = 1)
(Supplierj = i)
The capacity constraints can then be stated with
where Capi is defined defined above10.3.1.i
{1,..., 5} : Capi
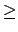
Suppliesi, j
We choose to determine the variables Costi by branching. Because no entry in a row of the cost matrix occurs twice, we immediately know which store is supplied by which warehouse. We select the variable Costi first for which the difference between the smallest possible value and the next higher value is maximal. Thus, decisions are made early in the search tree where the difference between two costs by different suppliers are maximal. The branching strategy will try the minimal value in the domain of Costi first. In Operations Research this strategy is known as the principle of least regret.
val capacity = #[3,1,4,1,4];
val costmatrix =
#[#[36,42,22,44,52],#[49,47,134,135,121],
#[121,158,117,156,115],#[8,91,120,113,101],
#[77,156,98,135,11],#[71,39,50,110,98],
#[6,12,120,98,93],#[20,120,25,72,156],
#[151,60,104,139,77],#[79,107,91,117,154]];
val maxValue = (valOf (Int.maxInt))div 2
fun warehouse cap costm space =
let
val isopen as #[o1,o2,o3,o4,o5] =
FD.boolvarVec(space,5)
val supplier as #[s0,s1,s2,s3,s4,s5,s6,s7,s8,s9] =
FD.rangeVec(space,10,(0,4))
val cost as #[c0,c1,c2,c3,c4,c5,c6,c7,c8,c9] =
FD.rangeVec(space,10,(1,1000))
val suppliesij = Vector.tabulate(5,fn x =>
FD.boolvarVec(space,10))
val sumcost = FD.range(space,(1,10000))
val nbopen = FD.range(space,(0,5))
val totalcost = FD.range(space,(1,11000))
fun order(curr,last)=
post (curr, FD(totalcost)`<
`(FD.Reflect.value(last,totalcost)),FD.BND)
in
(* posts sum of isopen[i] = nbopen *)
post(space,SUMV(Vector.map(fn x =>
FD.boolvar2intvar x)isopen) `= FD(nbopen),FD.DOM);
(* posts sum of cost[i]= sumcost *)
post(space,SUMV(cost) `= FD(sumcost),FD.DOM);
post(space,FD(sumcost)`+ FD(nbopen) `* `50
`= FD(totalcost),FD.DOM);
(* ensures that for i={1,..,5}and j={1,..,10}:
supplies_{i,j} = 1 <-> supplier[j]=i *)
let
val tmp = Vector.concat(Vector.toList
(Vector.tabulate(5,fn x =>
Vector.tabulate(10,fn y =>(x,y)))))
in
Vector.app(fn(i,j) =>
FD.Reified.relI(space,
Vector.sub(supplier,j),FD.EQ,i,
Vector.sub(Vector.sub(suppliesij,i),j)))
tmp
end;
(* ensures that for i ={1,..,5}and j={1,..,10}:
capacity[i] >= sum supplies_{i,j} *)
Vector.app(fn(x) =>
post(space,SUMV(Vector.map(fn y =>
FD.boolvar2intvar y)(Vector.sub(suppliesij,x)))
`<= `(Vector.sub(cap,x)),FD.DOM))
(#[0,1,2,3,4]);
(* ensures that cost[i] = costmatrix_{i,(supplier[i])} *)
Vector.appi(fn(i,x) => FD.elementI( space,x,
Vector.sub(supplier,i),Vector.sub(cost,i)))
(costm);
(* ensures that open[i]= 1 <->
W_i does support at least one store *)
Vector.appi(fn(i,x) =>
let
val tmp = Vector.map(fn y => FD.boolvar2intvar y)x
val tmp2 = FD.range(space,(0,5))
in
post(space,SUMV(tmp) `= FD(tmp2),FD.DOM);
FD.Reified.relI(space,tmp2,FD.GR,0, Vector.sub(isopen,i))
end)
(suppliesij);
FD.branch(space,cost,FD.B_REGRET_MIN_MAX,FD.B_MIN);
({cost,totalcost,supplier,suppliesij,isopen,nbopen},order)
end
Andreas Rossberg 2006-08-28