6.7 Disjunctive Propagator

In Oz, a disjunctive propagator has the form:

or C1 [] C2 end

and its declarative semantics is simply that of disjunction. In LP, the only method available for dealing with complex disjunctions of that kind is non-determinism. Thus in Prolog, you would would write:

C1 ; C2

Operationally, this means: first try C1 and if that fails backtrack and try C2 instead. This has several drawbacks: (1) it is not sound (failure to prove 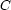is not the same as proving 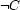$\neg C$ ), (2) it forces the computation to commit immediately to exploring either one alternative or the other.

Early commitment is a poor strategy. It is often preferable to delay a choice until sufficient information is available to reject one of the alternatives. This is the intuition underlying the disjunctive propagator: or C1 [] C2 end is a propagator not a choice point. It blocks until either C1 or C2 becomes inconsistent with respect to the current store of basic constraints: at that point, the propagator commits, i.e. reduces to, the remaining alternative. In this way, a disjunctive propagator has the declarative semantics of sound logical disjunction, unlike Prolog's ; operator which implements merely negation as failure. The operational semantics are given by the rules below, where 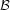$\mathcal{B}$ represents the current basic constraints:

$\begin{array}{@{}rll@{}} \mathcal{B}\wedge C_1&\rightarrow^*&\textsf{false}\\\hline \mathcal{B}\wedge(C_1\ \textbf{or}\ C_2)&\rightarrow&\mathcal{B}\wedge C_2\\[2mm] \mathcal{B}\wedge C_2&\rightarrow^*&\textsf{false}\\\hline \mathcal{B}\wedge(C_1\ \textbf{or}\ C_2)&\rightarrow&\mathcal{B}\wedge C_1 \end{array}$

This is realized by taking advantage of nested computation spaces. A disjunctive propagator or C1 [] C2 end creates 1 nested space to run C1 and another to run C2 and constantly monitors their status (either entailed or failed). When for example the space running C1 is discovered to be failed, then the disjunctive propagator commits to the other space, i.e. it merges the contents of the space running C2 with the current space. When this is done the propagator disappears (we also say that it reduces).

A disjunctive propagator blocks until it reduces. This is why, in Oz programs, disjunctive propagators are usually spawned in their own thread to allow the rest of the computation to proceed. In effect, this makes a disjunctive propagator into a concurrent agent:

thread or C1 [] C2 end end

A disjunctive propagator commits to one alternative only when the other becomes inconsistent. But, when neither becomes willingly inconsistent, it is often necessary, in the interest of completeness, to non-deterministically enumerate the alternatives. This can easily be achieved by introducing a control variable X:

or X=1 C1 [] X=2 C2 end

We can now apply a distribution strategy on FD variable X to force exploration of the alternatives. In a typical program, you might often invoke first a distribution strategy on the variables of the CSP, and then a second distribution strategy on the control variables to make sure for the sake of completeness that all disjunctions have been decided:

%% distribute on the variables of the CSP {FD.distribute ff [I1 I2 I3]} %% distribute on the control variables {FD.distribute ff [X1 X2]}