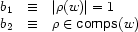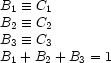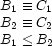6.8 Reified Constraints
There are often cases when, instead of imposing a constraint 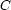 , we want to speak (and possibly constrain) its truth value. Let's take an example from Chapter 5: the cardinality of a daughter set
, we want to speak (and possibly constrain) its truth value. Let's take an example from Chapter 5: the cardinality of a daughter set 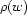 is at most 1, and it is 1 iff
is at most 1, and it is 1 iff  is required by
is required by 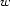 's valency, i.e if
's valency, i.e if 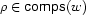 . Let
. Let 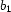 stand for the truth value of
stand for the truth value of 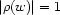 and
and 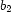 stand for the truth value of
stand for the truth value of 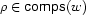 :
:
The well-formedness condition mentioned above is expressed simply by 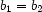 .
.
For the purpose of this section, we will write 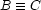 to represent a reified constraint, where
to represent a reified constraint, where 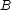 is a FD variable representing the truth value of constraint
is a FD variable representing the truth value of constraint 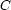 : 0 means false, 1 means true. The operational semantics are as follows:
: 0 means false, 1 means true. The operational semantics are as follows:
if
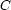 is entailed then
is entailed then 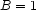 is inferred
is inferredif
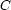 is inconsistent then
is inconsistent then 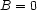 is inferred
is inferredif
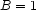 is entailed, then
is entailed, then 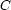 is imposed
is imposedif
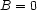 is entailed, then
is entailed, then 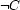 is imposed
is imposed
For example, here is how reified constraints can express that exactly one of 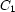 ,
, 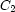 , and
, and 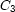 must hold:
must hold:
Similarly, here is how to express 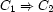 :
:
The astute reader may wonder ``why do we need a new concept? can't we express reified constraints in terms of disjunctive propagators?''. Indeed, 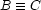 can also be written:
can also be written:
or B=1 C [] B=0 ~C end where somehow ~C is intended to represent the negation of C. What makes reified constraints attractive is that they are much more efficient. A disjunctive propagator needs to create 2 nested spaces, but a reified constraint doesn't need any.
In the libraries of the Mozart system, many constraints are also available as reified constraints (but not all). For example:
{FS.reified.include I S B} B represents the truth value of {FS.include I S}. If B=0, the reified constraint reduces to {FS.exclude I S}.