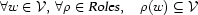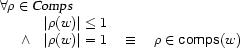5.4.3 Valency Constraints
Every daughter set is a finite set of nodes in the tree:
The second principle of well-formedness requires that a complement daughter set 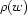 be non-empty only when
be non-empty only when  appears in
appears in 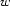 's valency. Additionally, the first principle states that, when it is non-empty, the complement daughter set
's valency. Additionally, the first principle states that, when it is non-empty, the complement daughter set 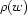 must be a singleton:
must be a singleton:
In practice, the equivalence above will be enforced using reified constraints which are explained in Section 6.8.