Example: Fractions

Problem Specification

The Fractions Puzzle consists in finding distinct nonzero digits such that the following equation holds:

${\frac{{A}}{{BC}}}$ + ${\frac{{D}}{{EF}}}$ + ${\frac{{G}}{{HI}}}$ = 1

Viewpoint and Constraints

We have a variable for every letter, similar as in the Send More Money Puzzle. Since the three fractions are symmetric, we can impose the order

${\frac{{A}}{{BC}}}$$\ge$${\frac{{D}}{{EF}}}$$\ge$${\frac{{G}}{{HI}}}$

From the order constraints we obtain the redundant constraints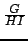

3${\frac{{A}}{{BC}}}$$\ge$1 and 3${\frac{{G}}{{HI}}}$$\le$1

The order constraints together with the redundant constraints reduce the size of the search tree by one order of magnitude.

Branching Strategy

We branch on the list of letters using the standard first-fail strategy.

Script

fun fractions space =
        let 
            val letters as #[a,b,c,d,e,f,g,h,i]=
                FD.rangeVec(space,9,(1,9))
            val bc = FD.range(space,(1,81))
            val ef = FD.range(space,(1,81))
            val hi = FD.range(space,(1,81))
        in
            FD.distinct(space, letters, FD.DOM);
            post(space,`10 `* FD(b) `+ FD(c) `= FD(bc),FD.DOM);
            post(space,`10 `* FD(e) `+ FD(f) `= FD(ef),FD.DOM);
            post(space,`10 `* FD(h) `+ FD(i) `= FD(hi),FD.DOM);   
            post(space,FD(a) `* FD(ef) `* FD(hi) `+
                       FD(d) `* FD(bc) `* FD(hi) `+
                       FD(g) `* FD(bc) `* FD(ef) `= 
                       FD(bc) `* FD(ef) `* FD(hi),FD.DOM);
            (* impose canonical order *)
            post(space,FD(a) `* FD(ef) `>= FD(d) `* FD(bc),FD.DOM);
            post(space,FD(d) `* FD(hi) `>= FD(g) `* FD(ef),FD.DOM);
            (* redundant constraints *)
            post(space,`3 `* FD(a) `>= FD(bc),FD.DOM);
            post(space,`3 `* FD(g) `<= FD(hi),FD.DOM);
            FD.branch(space,letters,FD.B_SIZE_MIN,FD.B_MIN);
            {letters}  
       end

The script constrains its problem variable letters to a vector having a field for every letter. Since Alice has no finite domain propagators for fractions, we eliminate the fractions by multiplying with the denominators. For every denominator we introduce an auxiliary variable.