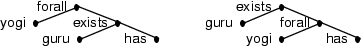4 Dominance Constraints
Trees are widely used for representing hierarchically organized information, such as syntax trees, first-order terms, or formulae representing meanings. A tree can be regarded as a particular type of directed graph. A directed graph is a pair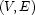 
where 
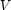is a set of vertices and 
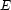a multiset of directed edges between them, i.e. a subset of 
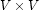. A forest is an acyclic graph where all vertices have in-degree at most 1. A tree is a forest where there is precisely one vertex, called the root, with in-degree 0; all others have in-degree 1.
First-order terms, or finite constructor trees, are characterized by a further restriction: each node is labeled by some constructor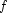 
of a signature 
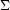, and its out-edges are labeled by integers from 1 to n, where n is the arity of the constructor. This can be formalized as follows: we assume a signature 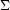of function symbols 
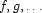, each equipped with an arity 
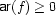. A finite constructor tree is then a triple 
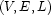where 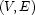defines a finite tree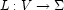, and 
and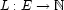 
are labelings, and such that for any vertex 
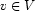there is exactly one outgoing edge with label 
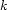for each 
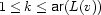and no other outgoing edges.
Trees are often used to represent syntactic structure. For example, here is a possible analysis of "beans, John likes everyday".
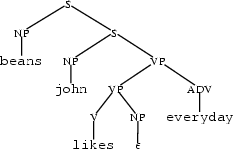
or logical formulae representing meanings. For example, here are the simplified representations of the two meanings of the ambiguous sentence "every yogi has a guru":
